图的基本概念与表示
在分析图结构前,需明确图的核心组成要素和常见表示方法:
核心组成
- 顶点(Vertex)
图中的节点,通常用数字或字母表示(如顶点1、2、3或A、B、C)。
- 边(Edge)
连接顶点的线,分为无向边(双向可达)和有向边(单向可达,带箭头)。
图的表示方法
- 邻接表
用列表记录每个顶点的相邻顶点(适合稀疏图,节省空间)。
- 邻接矩阵
用二维矩阵表示顶点间的连接关系(适合稠密图,查询高效)。
提示:选择表示方法时,需权衡空间和时间效率。稀疏图(边数少)优先用邻接表,稠密图(边数多)优先用邻接矩阵。
图结构分析的核心步骤
确定图的类型
有向图 vs 无向图
有向图
边有方向(如社交网络的"关注"关系),用箭头表示方向。
例:(A→B) 表示仅A可指向B
无向图
边无方向(如社交网络的"好友"关系),双向可达。
例:(A,B) 表示A和B可互相到达
是否含环
有环图
存在从某顶点出发,沿边可回到自身的路径。
例:A→B→C→A
无环图
不存在上述路径,如DAG(有向无环图)。
判断技巧:有向图可通过拓扑排序验证
是否连通
连通图(无向图)
任意两顶点间都有路径可达。
强连通图(有向图)
任意两顶点u和v,既存在u到v的路径,也存在v到u的路径。
弱连通图(有向图)
忽略边的方向后为连通图,但不满足强连通。
解析顶点的度(Degree)
"度"是顶点的核心属性,反映顶点与其他顶点的连接强度:
无向图的度
顶点的度 = 与该顶点相连的边的数量(如顶点A连接B、C,则度为2)。
有向图的度
- 入度:以该顶点为终点的边的数量(被指向的次数)。
- 出度:以该顶点为起点的边的数量(指向他人的次数)。
例:若有边A→B、B→C、A→C,则B的入度=1(A→B),出度=1(B→C)。
分析边的关系与路径
边的权重(若有)
带权图中,边的数值表示成本、距离等(如交通图中边的权重表示距离),需记录权重信息用于路径计算(如最短路径)。
路径与回路
- 路径:从顶点u到v的一系列边组成的序列(如A→B→C是A到C的路径)。
- 简单路径:路径中顶点不重复的路径。
- 回路(环):起点和终点相同的路径(如A→B→A)。
关键路径(针对DAG)
在带权DAG中,从起点到终点的最长路径,常用于项目调度分析(如任务依赖的最短完成时间)。
识别特殊子结构
图中可能包含具有特殊意义的子结构:
子图
由原图的部分顶点和边组成的图(顶点和边均为原图的子集)。
树
无环的连通无向图(n个顶点必有n-1条边),任意两顶点有且仅有一条路径。
生成树
包含原图所有顶点的子图,且为树(用于网络布线等场景)。
强连通分量(SCC)
有向图中最大的强连通子图(子图内任意两顶点互达)。
实例分析:有向无环图(DAG)
以边集为 (1,2)、(1,3)、(2,4)、(3,4) 的有向图为例,按步骤分析:
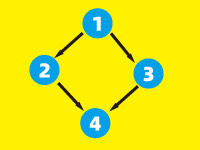
图结构示意图
1. 确定类型
- 有向图(边有方向,带箭头)
- 无环图(无从顶点出发回到自身的路径)
- 连通性:忽略方向后所有顶点相连(弱连通),但非强连通(如4无法到达其他顶点)
2. 顶点的度
| 顶点 | 入度 | 出度 |
|---|---|---|
| 1 | 0 | 2(→2、→3) |
| 2 | 1(←1) | 1(→4) |
| 3 | 1(←1) | 1(→4) |
| 4 | 2(←2、←3) | 0 |
3. 路径分析
- 从1出发的路径:1→2→4、1→3→4、1→2、1→3
- 从2出发的路径:2→4
- 从3出发的路径:3→4
- 从4出发的路径:无(出度为0)
- 无回路(符合DAG特征)
4. 依赖关系
1是2、3的前驱,2、3是4的前驱,2和3无依赖关系。
常用分析工具与算法
可视化工具
- 手绘草图
适合简单图的快速分析,直观易懂。
- Graphviz
通过代码描述图结构,自动生成可视化图形。
- Visio / Draw.io
交互式绘图工具,适合复杂图的可视化展示。
算法辅助
- DFS/BFS
遍历图,判断连通性、检测环。
- 拓扑排序
验证DAG并确定顶点执行顺序。
- Kosaraju算法
寻找有向图的强连通分量。
- Prim/Kruskal算法
构建最小生成树,优化网络结构。
总结
分析图结构的核心是"拆解":先明确图的类型和基本属性(顶点、边、度),再分析顶点间的连接关系(路径、依赖),最后识别特殊子结构。无论是手工分析还是编程实现,清晰的步骤和对基本概念的理解都是关键。

